| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
O.B., 3/05/2007, Créé avec GeoGebra
Exercice 1 d'application :
Pour un verre d'indice nv=1,5 et une longueur d'onde de 560 nm :
1/ Déterminer à l'aide du curseur l'indice nc que doit avoir l'antireflet.
2/ Vérifier ce résultat par calcul.
Pour un verre d'indice nv=1,5 et une longueur d'onde de 560 nm:
1/ Déterminer en déplaçant le point G, la plus petite épaisseur que doit avoir l'antireflet.
2/ Vérifier ce résultat par calcul.
Exercice 3 d'application :
Sur un verre d'indice nv=1,604 on réalise un antireflet d'indice nc=1.38. La longueur d'onde de référence est de 560 nm :
1/ Déterminer l'épaisseur minimale à donner à l'AR.
2/ Grâce à l'animation que pouvez vous en conclure sur l'intensité réfléchie et l'efficacité de cet AR ?
3/ Sachant que les coefficient de réflexion sont :
a/ Calculer ces coefficients de réflexion.
b/ En déduire l'intensité maximale Imax pouvant être réfléchie. On prendra l'amplitude de l'onde incidente a=1.
c/ Calculer l'intensité résiduelle relative réfléchie IR pour l'épaisseur minimale de l'AR. On rappelle : IR=I/Imax.
4/ Quel devrait être l'indice de l'antireflet ?

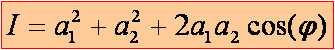
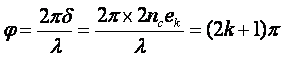 k
entier
k
entier